Formal Analysis of Unmanned Aerial Vehicles using Higher-order-logic Theorem Proving
Abstract
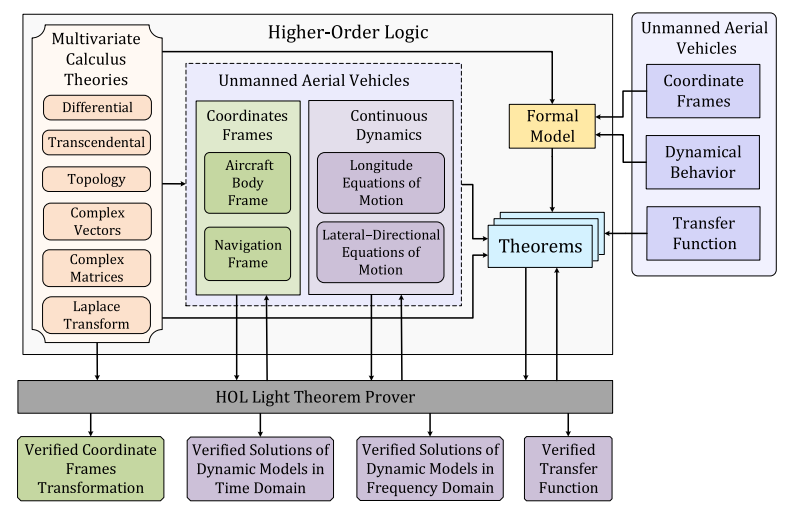
The continuous dynamics of Unmanned Aerial Vehicles (UAVs) are generally modeled as a set of differential equations. Traditionally, these continuous dynamics of UAVs are analyzed using paper-and-pencil proof and computer-based testing or simulations to study the performance, stability, and various other control characteristics of the aircraft flying in the air. However, these techniques suffer from their inherent limitations such as human error-proneness, sampling based analysis, approximations of the mathematical results and the usage of unverified algorithms. Thus, these methods cannot be trusted, considering the utility of UAVs in many safety-critical applications. To overcome the limitations of the above-mentioned techniques, we propose to use higher-order-logic theorem proving for formally analyzing the continuous dynamics of UAVs. In particular, we provide a formalization of complex-valued matrices in higher-order logic using the HOL Light theorem prover, which is in turn used for the formalization of the navigation and aircraft’s body-fixed frames and their associated transformations. We also provide formal reasoning support for analyzing the Multiple-input Multiple-output (MIMO) systems, which are in turn used for formally analyzing the continuous dynamics of UAVs using HOL Light. For illustration, we use our proposed framework for the formal stability analysis of the CropCam UAV using HOL Light.
Framework
People
- Adnan Rashid, SEECS, NUST, Pakistan
- Osman Hasan, SEECS, NUST, Pakistan
- Sa'ed Abed, Kuwait University, Kuwait
Publications
- A. Rashid, O. Hasan and Sa'ed Abed, “Using an Interactive Theorem Prover for Formally Analyzing the Dynamics of the Unmanned Aerial Vehicles”, Mobile Robot: Motion Control and Path Planning, pp: 253-282, Chapter 9, Studies in Computational Intelligence (SCI) Series, Vol. 1090, Springer, 2022.
- Sa'ed Abed, A. Rashid and O. Hasan, “Formal Analysis of Unmanned Aerial Vehicles using Higher-order-logic Theorem Proving”, Journal of Aerospace Information Systems, Vol. 17, No. 9, pp. 481-495, DOI:10.2514/1.I010730, 2020.