Abstract

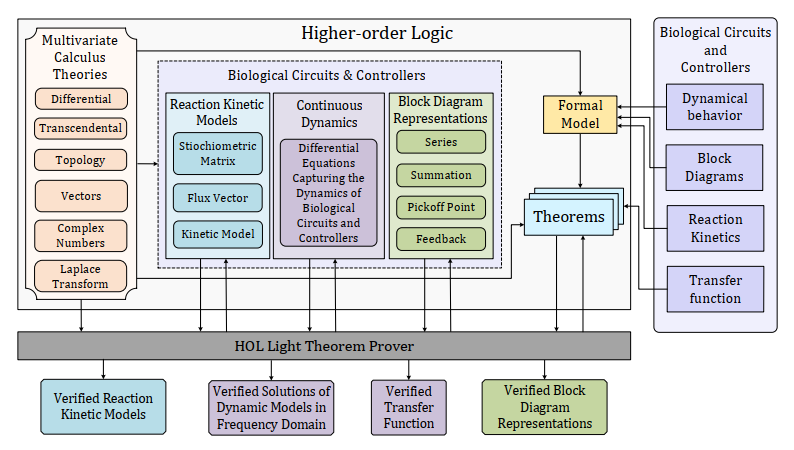
Synthetic Biology is an interdisciplinary field that uses well-established engineering principles, ranging from electrical, control and computer systems, for analyzing the biological systems, such as biological circuits, enzymes, pathways and controllers. Controllers play a pivotal role in regulating different components and modules of a biological system thus ensure its smooth functionality. They are commonly used in the genetic circuits and other biological organisms. Traditionally, these biological systems, i.e., the genetic circuits and their associated controllers are analyzed using paper-and-pencil proofs and computer-based simulations methods. However, these techniques cannot provide accurate results due to their inherent limitations such as human error-proneness, round-off errors and the unverified algorithms present in the core of the tools, providing such analyses. We propose to use higher-order-logic theorem proving as a complementary technique for analyzing these systems and thus overcome the above-mentioned issues. It is based on developing a mathematical model of the underlying system based on an appropriate logic and analyzing it using deductive reasoning. The involvement of the mathematics and the logical reasoning in this method ensures the accuracy of the analysis. In this project, we propose a higher-order-logic theorem proving based framework to formally reason about the genetic circuits and their associated controllers used in synthetic biology. The main idea is to, first, model the continuous dynamics of the genetic circuits and their associated controllers using differential equations. These dynamics are generally obtained from the reaction-based models of these systems and thus requires the notion of reaction kinetics. The next step is to obtain the systems’ transfer function from their corresponding block diagram representations. Finally, the transfer function based analysis of these differential equation based models is performed using the Laplace transform, which is further used for the stability analysis of these systems. To illustrate the practical utilization of our proposed framework, we formally analyze the genetic circuits of activated and repressed expressions and autoactivation of protein, and phase lag and lead controllers.

Framework

People

• Adnan Rashid, SEECS, NUST, Pakistan
• Osman Hasan, SEECS, NUST, Pakistan
• Sa'ed Abed, Kuwait University, Kuwait

Publications

1. Sa'ed Abed, A. Rashid and O. Hasan, “Formal Analysis of the Biological Circuits using Higher-order-logic Theorem Proving”, ACM/SIGAPP Symposium On Applied Computing (SAC), pp. 355-360, Brno, Czech Republic, 2020.
2. Sa'ed Abed, A. Rashid and O. Hasan, “ Formal Reasoning about Synthetic Biology using Higher-order-logic Theorem Proving”, IET Systems Biology, Volume. 14, No. 5, pp. 271-283, DOI:10.1049/iet-syb.2020.0026, 2020.